티스토리 뷰
과학사의 연대기에서 스코틀랜드의 물리학자 제임스 클러크 맥스웰만큼 지울 수 없는 족적을 남긴 사람은 거의 없습니다. 그는 전자기학 분야에서 획기적인 연구를 통해 우주를 지배하는 근본적인 힘에 대한 우리의 이해에 혁명을 일으켰습니다. 맥스웰의 전자기학 이론은 4개의 우아한 방정식으로 요약되어 현대 물리학의 토대를 마련했으며 알버트 아인슈타인의 상대성 이론 발전에 큰 영향을 미쳤습니다. 이 기사에서 우리는 Maxwell의 전자기 이론을 통한 여행을 시작하여 핵심 원리, 실제 응용 프로그램 및 혁신적인 상대성 이론에 대한 심오한 영향을 탐구합니다.
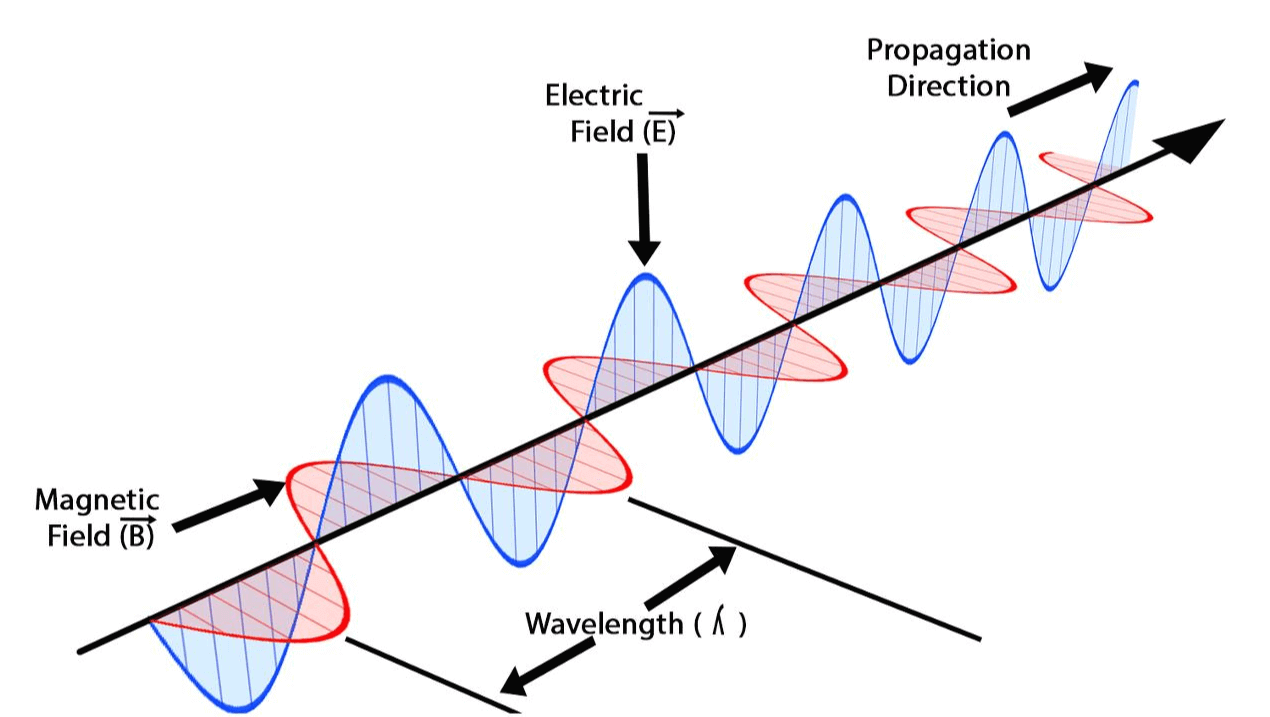
전기와 자기의 합일
맥스웰 시대 이전에 전기와 자기는 별개의 현상으로 간주되었으며 각각 고유한 일련의 법칙과 원리가 적용됩니다. 그러나 맥스웰의 천재성은 이 두 힘 사이의 깊은 연관성을 인식하는 데 있었습니다. 그는 전기장과 자기장이 고립된 실체가 아니라 단일 전자기력의 상호 관련된 측면이라고 가정했습니다.
맥스웰의 전자기 이론은 현재 맥스웰 방정식으로 알려진 일련의 네 가지 기본 방정식을 도입했습니다. 이 방정식은 전기장과 자기장의 거동과 그 상호 작용을 수학적으로 설명합니다. 이 방정식은 변화하는 전기장이 자기장을 생성하고 그 반대의 경우도 마찬가지이며 전자기파가 일정한 속도, 즉 빛의 속도로 전파된다는 것을 보여주었습니다.
4개의 맥스웰 방정식은 다음과 같습니다.
전기에 대한 가우스의 법칙
적분 형태: ∮ E · dA = Q / ε₀
미분 형식: ∇ · E = ρ / ε₀
전기에 관한 가우스의 법칙에서 E는 전기장 벡터, Q는 폐곡면으로 둘러싸인 총 전하, ε₀은 진공 유전율(전기 상수), ∮는 표면 적분, ∇·E는 전기장 벡터의 발산을 나타냅니다. 방정식은 닫힌 표면을 통과하는 전기 플럭스가 진공 유전율로 나눈 표면으로 둘러싸인 총전하와 같다고 말합니다.
자기에 대한 가우스 법칙
적분 형태: ∮ B · dA = 0
미분 형식: ∇ · B = 0
자기에 대한 가우스의 법칙에서 B는 자기장 벡터를 나타내고 ∮는 표면 적분을 나타냅니다. 이 방정식은 닫힌 표면을 통과하는 자속이 0이라고 명시하며 이는 자연에 자기 모노폴(단일 자기 전하)이 없음을 나타냅니다.
패러데이의 전자기 유도 법칙
적분형 : ∮ E · dl = - dΦB/dt
미분 형식: ∇ × E = - ∂B / ∂t
패러데이의 전자기 유도 법칙은 폐루프(루프 주변의 전기장 E의 선적분으로 표시됨)에서 유도된 전기장을 루프를 통과하는 자속의 변화율(dΦB/dt)과 관련시킵니다. 방정식은 변화하는 자기장이 전기장을 유도한다는 것을 보여줍니다.
암페어의 회로 법칙
적분형 : ∮ B · dl = μ₀(I + ε₀ dΦE/dt)
미분 형식: ∇ × B = μ₀J + μ₀ε₀ ∂E / ∂t
앙페르의 회로 법칙은 폐루프 주변의 자기장 B(루프 주변의 자기장 B의 선 적분으로 표시)를 루프를 통과하는 총 전류 I와 루프를 통과하는 전기 플럭스의 변화율(dΦE/dt)과 관련시킵니다. 방정식은 변화하는 전기장이 자기장을 생성한다는 것을 보여줍니다.
이 방정식에서 E는 전기장 벡터를 나타냅니다. B는 자기장 벡터를 나타냅니다. ρ는 전하 밀도입니다. J는 전류 밀도입니다. ε₀은 진공 유전율(전기 상수)입니다. μ₀는 진공 투자율(자기 상수)입니다. ∇는 기울기 또는 발산 연산자를 나타내는 del 연산자입니다. ∮는 폐곡면 적분, ∮ dl은 폐루프 적분을 의미합니다.
전자기파의 전파
맥스웰 이론의 가장 놀라운 결과 중 하나는 빛의 속도로 공간을 전파하는 전자기파의 예측이었습니다. 맥스웰은 전자기파의 속도를 수학적으로 도출했고 그것이 빛의 속도와 같다는 것을 발견하여 빛 자체가 전자기 복사의 한 형태임을 시사했습니다.
이러한 전기, 자기, 빛의 통합은 전파, 극초단파, 적외선, 가시광선, 자외선, X선, 감마선을 포함하는 전자기 스펙트럼을 이해하는 기반을 마련했습니다. 맥스웰의 연구는 빛의 파동적 특성을 입증했을 뿐만 아니라 각각 고유한 특성과 용도를 가진 전자기파의 전체 스펙트럼의 존재를 밝혀냈습니다.
상대성 이론에 대한 맥스웰의 영향
맥스웰의 전자기학에 관한 획기적인 연구는 현대 물리학의 발전, 특히 알베르트 아인슈타인의 상대성 이론 공식화에 지대한 영향을 미쳤습니다.
맥스웰의 방정식은 빛을 포함한 전자기파가 진공에서 일정한 속도, 즉 'c'로 표시되는 빛의 속도로 전파된다는 것을 보여주었다. 이 일정한 빛의 속도는 광원이나 관찰자의 움직임과 무관했습니다. 이 통찰력은 절대적인 공간과 시간이라는 고전적 개념에 중대한 도전을 제기했습니다.
맥스웰의 방정식과 빛의 속도가 일정하다는 개념에서 영감을 받은 알버트 아인슈타인은 1905년에 특수 상대성 이론을 발전시켰습니다. 아인슈타인의 이론은 물리 법칙이 등속 운동을 하는 모든 관찰자에게 동일하다는 것을 제안하고 시간 팽창 및 길이 수축과 같은 공간과 시간에 대한 혁신적인 아이디어를 도입했습니다.
1915년 아인슈타인은 중력을 포함하도록 이론을 확장하여 일반 상대성 이론을 탄생시켰습니다. 이 이론은 중력을 질량과 에너지의 존재로 인해 발생하는 시공간 곡률로 재구성했습니다. Maxwell의 작업은 상수 'c'가 아인슈타인 공식화에서 중추적인 역할을 했기 때문에 일반 상대성 이론의 발전에 간접적으로 영향을 미쳤습니다.
결론
James Clerk Maxwell의 전자기 이론은 인간의 지성과 호기심의 힘에 대한 증거입니다. 그의 전기와 자기의 통합, 전자기파의 예측, 빛의 항속성 유도는 현대 물리학의 토대를 마련했습니다. 빛을 전자기파로 이해하도록 이끈 맥스웰의 연구는 알버트 아인슈타인의 상대성 이론의 발전에 깊은 영향을 미쳤습니다. 맥스웰의 전자기 이론과 아인슈타인의 상대성 이론 사이의 심오한 연결은 과학적 아이디어의 상호 연결성과 우주에 대한 이해의 지속적인 진화를 보여줍니다. Maxwell의 유산은 그의 이름이 붙은 기본 방정식을 통해 지속되며, 물리학 및 공학 분야를 계속 형성하고 인간의 탐구와 발견의 탁월함을 입증합니다.
